8.4 循环神经网络

1. 原理

在 8.3 语言模型和数据集中我们研究了 N-gram 语言模型，会随着 N 的增长空间复杂度越来越大，不如我们假设给定一个句子，下一个词出现和两个因素有关：

• 最近的那个 token
• 这段句子除最近那个 token 以外其余 token 的总结（状态）

这个状态和句子里 token 的顺序强相关，只要 token 的顺序确定的，状态值就确定了

“I love you” 后面生成 2 个单词，RNN 示意图，所以该网络输入的是前一个时刻的状态，和当前时刻 token 的值

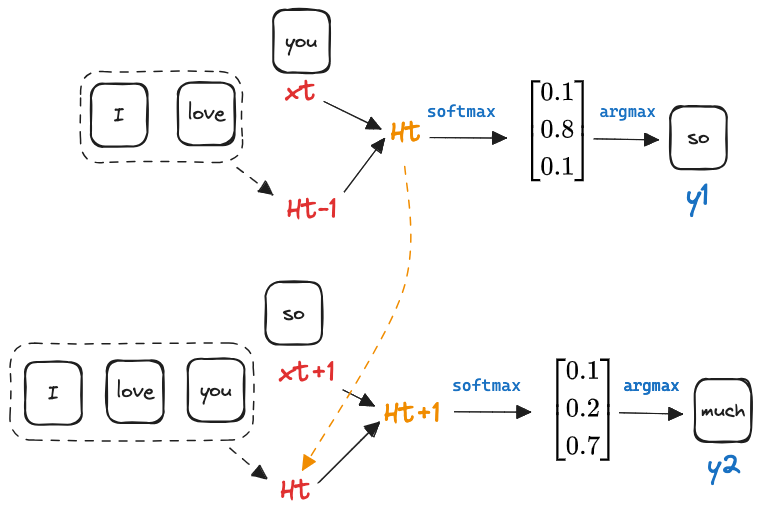
如上图所示，这个网络的输入为 ：

• 前一个时刻的状态 $H_{t-1}$
• 当前时刻 token 的值 $x_t$

输出为：

• 这个时刻的状态 $H_t$
• 这个时刻的预测 $y$

为了简单起见，我们假定：

其中 $\varphi$ 是激活函数，对于输出 $y$，实际上是一个多分类问题，简单起见，利用 softmax 回归（3.4 softmax 回归），输出类别是状态的线性模型：

在最简单的假定下，输出 y 可以看做当前 token 的单隐藏层神经网络，只不过加入了状态的更新，在状态维度上来看，状态的更新可以看做多层全连接神经网络

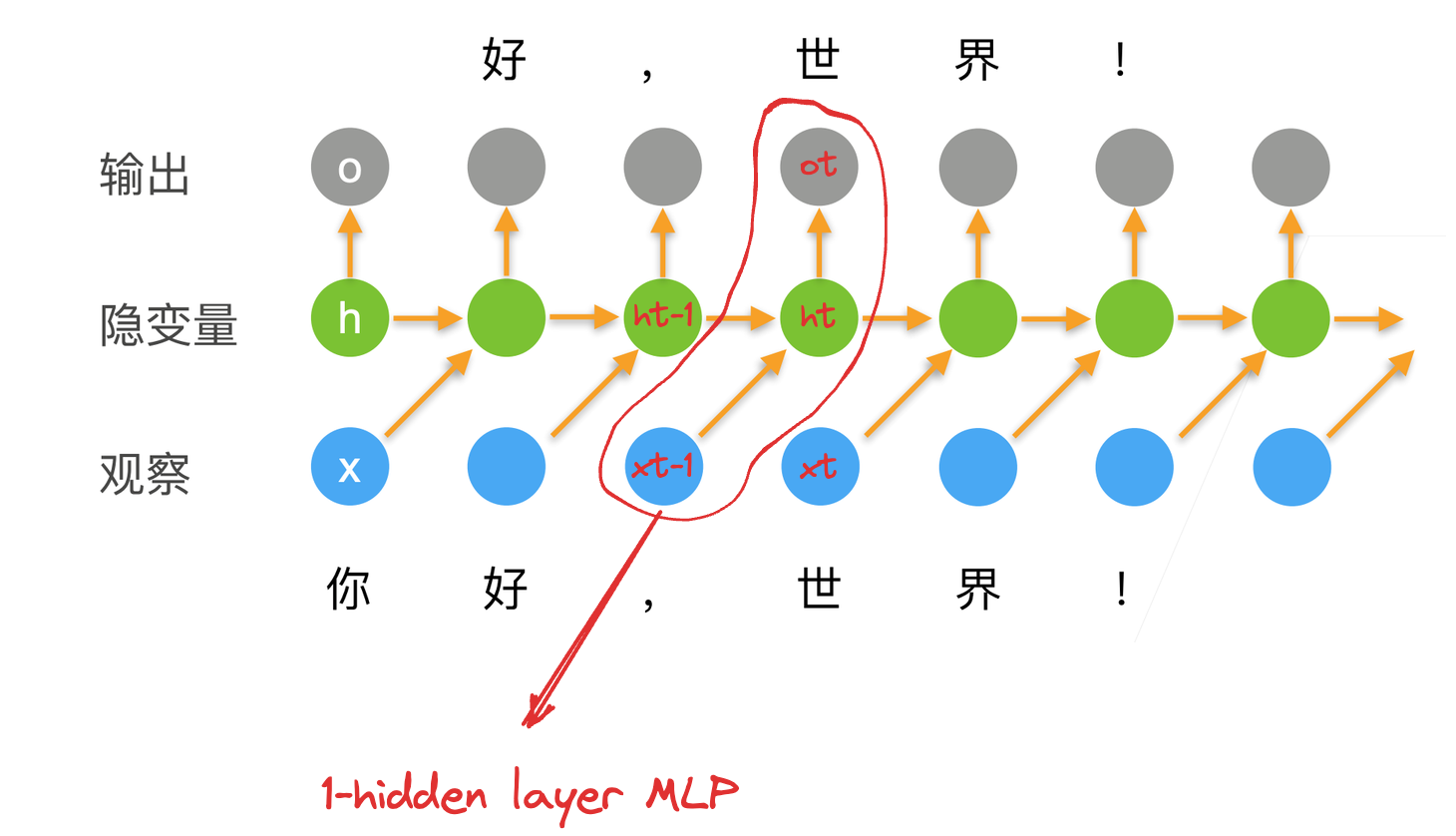
2. 困惑度

在上面模型中，利用了 softmax 回归，所以损失函数自然为交叉熵损失，给定一个预测序列，和实际序列作对比，每个时间步长都有一个损失，所以衡量模型的损失可以用平均交叉熵来衡量：

但由于历史原因，自然语言处理的科学家更喜欢使用一个叫做困惑度（perplexity）的量。简而言之，是上式的指数，这样可以放大这种损失：

困惑度最好的时候为 1，表示没有困惑，越大说明选某个词的困惑很大

参考文献